UNIDADES QUÍMICAS DE LA CONCENTRACIÓN DE LAS SOLUCIONES

Otra forma de expresar la concentración de las soluciones es mediante las unidades químicas. Estas unidades dependen del tipo de sustancia o sustancias que forman la solución. La concentración de una solución, empleando las unidades químicas, pueden expresarse de dos maneras: tomando como unidad la masa molecular o la masa de un equivalente-gramo.

 

 

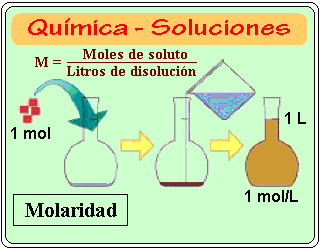
Molaridad o concentración molar (M): Es el número de moles de soluto contenido en un litro de solución. Se representa con la letra M y se encuentra dividiendo el número de moles de soluto (n) entre el volumen (v) en litro de la solución:

 

 

Ejemplos:

1. Se tiene 3.6 moles de azúcar en 1.8 litros de solución. ¿Cuál será su concentración molar?

 

Se puede realizar aplicando una regla de tres simple o aplicar la fórmula.

Aplicando la fórmula, tenemos que:

M = n / Litros de solución

M = 3.8 moles de azúcar / 1.8 Litros

M = 2 moles/L

2. Si tienes dos moles de NaCl para preparar una solución de 0.5 molar, ¿cuántos litros de ella se pueden preparar?

M = n / litros de solución

Despejando los litros de solución, tenemos:

litros de solución = n / M

litros de solución = 2 moles de NaCl / 0,5 M

litros de solución = 4 L

Molalidad o concentración molal (m): Es el número de moles de soluto contenidos en un kilogramo de disolvente. Se representa con la letra m y se expresa así:

 

Ejemplo: Determina la concentración molal de una solución preparada con 1.5 moles de una sal disueltos en 250 ml de agua.

Fijase que el disolvente está en ml, se debe hacer la conversión a kg, ya que son las variables que se manejan en la molalidad.

1000 ml de agua = 1000 gr de agua

1 kg = 1000 gr, por lo tanto, 1 kg de agua = 1000 ml de agua.

m = 0.15 moles de sal / 0.25 kg de agua

m = 6 moles/kg

Respuesta: La solución tiene una concentración de 6 molal.

Normalidad (N): Relaciona el número de equivalentes en gramo de un soluto, con la cantidad de solución, en litro.

El concepto de equivalente gramo ha sido desarrollado especialmente para referirse a ácidos y bases, por lo tanto, un equivalente gramo es igual a la masa de las sustancias (ácido o base), que produce un mol de iones H+ (hidronios), en el caso de los ácidos o un mol de iones OH- (hidroxilo) en el caso de las bases.

Un equivalente gramo es igual al peso del compuesto sobre el peso molecular o masa de un equivalente, es decir, número de moles. En el caso de ácidos y bases que producen más de una mol H+ o OH-, como por ejemplo el H2SO4 o el Fe(OH)3, el peso de un equivalente gramo se calcula dividiendo su peso molecular en gramos del ácido o de la base entre el número de iones hidronios o hidroxilos respectivamente.

 

 

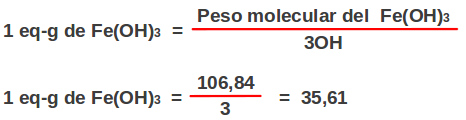
Ejemplo: ¿Cuál será la normalidad de una solución de NaOH que contiene 8 g de NaOH en 200 ml de solución?

eq-g de NaOH = 8 g ÷ 40 g/eq

eq-g de NaOH = 0.2

N = # eq-g de soluto ÷ volumen de la solución

N = 0.2 eq-g de NaOH ÷ 0.2 L de solución

N = 1eq-g/L

También se puede resolver por regla de tres simple:

1 mol de NaOH = 1 eq-g de NaOH

1 mol de NaOH = 40 gr/mol

1 eq-g de NaOH -------- 40 g

X ----------------- 8 g

X = 0,2 eq-g de NaOH

Se convierten los 200 ml a litros: 0,2 L.

N = 0,2 eq-g de NaOH / 0,2 L

N = 1eq-g/L

 

Fracción molar (Xi): se define como la relación entre las moles de un componente y las moles totales presentes en la solución. La fracción molar de la sustancia A (XA), componente de una solución, se define como el número de moles de la sustancia A dividido entre el número de moles totales de la solución (moles de soluto + moles de solvente).

 

Ejemplo: Una solución contiene 5.8 g de cloruro de sodio de NaCl y 100 g de H2O. Determina la fracción molar del agua y la sal.

Solución: convertimos los gramos de cada componente a moles.

n de NaCl = 5,8 g / 58,45 (g/mol)

n de NaCl = 0,09 mol

n de H2O = 100 g / 18 (g/mol)

n de H2O = 5,55 mol

Hallamos la fracción molar del agua y la sal:

XNaCl = 0,09 mol de NaCl / (0,09 mol de NaCl + 5,55 mol de H2O)

XNaCl = 0,09 mol de NaCl / 5,64 mol de la solución

XNaCl = 0,015

XH2O = 5,55 mol de H2O / (0,09 mol de NaCl + 5,55 mol de H2O)

XH2O = 0,09 mol de H2O / 5,64 mol de la solución

XH2O = 0,984